摘 要:电力变压器故障诊断因果关系的复杂性与模糊性,采用单一智能方法难以准确描述。文中基于智能互补融合的思想,将粗糙集理论与模糊Petri网络有机结合在一起进行油浸电力变压器故障诊断。利用粗糙集信息表简化技术来实现对专家知识的简化与故障特征的压缩,获得最小诊断规则,基于最小诊断规则的Petri网络模型可以有效降低网络结构的复杂性与故障特征获取的难度。同时利用模糊Petri网络实现并行模糊推理,便于描述故障特征的变化及对变压器运行特性的快速分析。故障实例分析表明,文中所提出的智能方法可以有效地进行模糊推理,减小诊断信息的冗余性,诊断效率高,计算快速、准确,结果易于被人理解。
关键词:变压器;故障诊断;粗糙集理论;模糊Petri网络
1 引言
电力变压器是电力系统厂站的关键设备,一旦发生故障,将带来巨大的经济损失。因此,建立智能诊断系统来保证变压器的安全可靠运行,具有非常重要的意义。
油浸电力变压器特征信号(如油色谱、介质损耗、铁心接地电流等)很多都能在不同方面反映变压器运行的状态。为提取这些特征信号来进行故障诊断,已提出了包括气相色谱法[1]、局部放电检测法[2]在内的多种故障检测方法。但由于每种特征信号反映故障均存在一定的局限性,就必须对多种检测方法提取的特征进行综合处理和协同分析,这是一个典型的信息融合过程。因此,基于专家系统、模糊理论、神经网络和Dempster-Shafer证据推理[3-6]等人工智能技术的油浸电力变压器故障综合诊断被广泛地研究。但是以上的这些方法往往都需要大量的统计信息与先验知识,因而计算、训练复杂,而实际变压器故障的复杂性与运行环境的恶劣,又造成了故障知识不完备或检测信息缺失,使得它们在诊断能力、适用性和知识获取方面还不尽人意,这就需要尝试应用一些新的智能技术进行变压器故障诊断[7-8]。同时,单一智能方法都具有自身的局限性,但结合使用可以实现智能互补,这是探索变压器故障诊断的一条新途径。
文献[8]提出了基于Petri网络的故障诊断方法,该方法可以将模糊启发式规则的表示和诊断能力融为一体,完成不确定性知识和过程性的模糊诊断推理,通过简单的矩阵运算即可快速获得诊断结果。但文中未提及建立Petri网络的规则是如何获得的,对于变压器故障诊断而言,建立专家系统所需的信息量非常大,因而所获得的专家知识中存在较大的冗余性,这在一定程度上影响了Petri网络建模的准确性和诊断的效率。针对上述问题,本文将粗糙集理论引入到变压器故障诊断中,利用其分析和处理不精确、不一致、不完整等不完备信息的能力,来发现专家知识间隐藏的关系,揭示潜在的规律,有效地简化了知识。同时进一步探讨了粗糙集与模糊Petri网络在知识表达上的优缺点及彼此间的互补性,基于智能互补融合的思想,将粗糙集理论与模糊Petri网络有机结合在一起进行油浸电力变压器故障诊断。故障实例分析表明,本文所提出的智能方法可以有效地进行智能推理,减小诊断信息的冗余性,提高了诊断效率。
2 基于粗糙集理论的知识约简
2.1 粗糙集理论简介
粗糙集理论(Rough Sets Theory,缩写为RST)是由Z. Pawlak于1982年提出的一种处理不完整性和不确定性问题的新型数学工具,能够在保留关键信息的前提下对知识进行处理,并求得知识的最小表达。
定U中每个对象属性值的信息函数,即f:U×A→Vq。由这种“属性-值”关系就构成了一张二维表,称之为信息表(Information Table)。
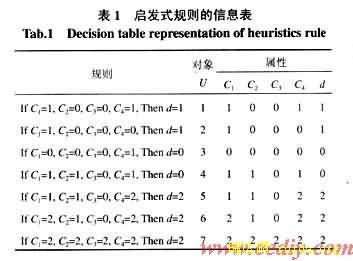
在RST中,知识是通过指定对象的基本特征(属性)和它的特征值(属性值)来描述的。通常启发式规则可以表示为IF-THEN结构,即条件-结论方式。如果用知识系统的条件属性表示规则的条件部分,决策属性表示规则的结论部分,则每一个对象可以方便地表示一条产生式规则。表1给出了规则对应的信息表。
2.2 知识约简
在根据启发式规则进行推理时,并非所有条件都是必要的,有些条件是相关的,有些条件是独立的,因而可能只需要某个或少量的条件就可以推断出结论。对信息表而言,并非所有的条件属性都是必要的,有些是多余的,去除这些属性不会影响原有的表达效果。如将表1中的属性C3去除,余下的属性仍能有效地分类,无规则冲突情况出现,这说明属性C3是冗余的。
因此,信息表知识约简是进行高效推理的关键。通过知识约简,可以获得最小化的推理规则,仅需使用少数必不可少的条件属性,通过简单推理便能获得与原信息表完全相同的结果。求解最小化规则的RST知识约简的步骤如下:
(1)删除表中相同的规则;
(2)基于协调性,约简表中条件同性集合的冗余属性,即消除表中多余的条件属性,得到最小属性集;
(3)基于协调法,约简表中各规则的冗余条件同性值,求出算法的核值表;
(4)基于核值表,约简表中的冗余规则,删除分类规则中多余的属性,只保留必要的属性;
(5)采用“在不同简化规则之间,相同简化规则合成一个子集合,不同简化规则用逻辑或运算符号∨合成一个子集合”的原则,得到一个或若干个最小规则集合。
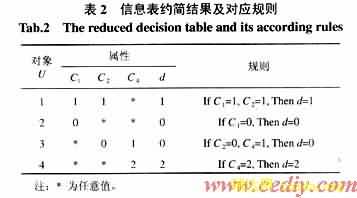
表2是按照以上步骤处理表1得到的约简结果,可见表2要比表1简单得多,但原有的知识表达和分类能力并没有改变。
3 基于模糊Petri网络的知识描述与推理
3.1 模糊Petri网络的定义
模糊Petri网络由两部分有向图组成,库所“Ο”和变迁“|”。考虑到库所存在的可能性与变迁的置信度,模糊Petri网络的结构定义如下:
定义2 N = (P, T, I, O, q, Fp, Ft)是一个七元式构成的网络。其中,P={p1, p2,…, pm}是库所的有限集合;T={t1,t2,…, tn}是变迁的有限集合;I:P→T是输入函数,是从库所到变迁的有向弧集合;O:T→P是输出函数,是从变迁到库所的有向弧集合;变迁的激发条件用托肯(token)实现,θ表示各库所中的托肯状态,即θ={θ1,θ2,…,θm};Fp={B(p1), B(p2),…, B(pm)}是库所的隶属函数,B(pj)是库所pj的隶属度;Ft={B(t1), B(t2),…, B(tn)}是变迁的隶属函数,B(ti)是变迁ti的置信度。
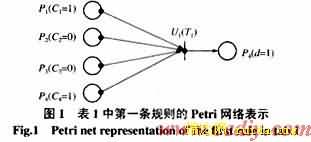
采用N描述产生式规则,网络的框架代表基于产生式规则的知识结构,库所表示命题,如果命题为真,在库所中标识上托肯,托肯的值表示命题为真的置信度;规则推理过程用模糊Petri网络中带置信度的变迁的触发表示,命题与推理规则之间的因果联系用库所和变迁之间的有向弧表示。表1中规则的Petri网表示如图1。
3.2 模糊Petri网络的矩阵模型
根据模糊Petri网络的定义和特点,可将模型进一步表达为N =(P,T,△,Γ,θ0,U),以便于推理计算。其中P、T的定义如上,其它采用矩阵形式表示,定义[10]如下:
定义3△:P→T为变迁的输入矩阵,△={δij},δij为逻辑量,δij∈{0,1},当Pi是Tj的输入时,即Pi到Tj间存在有向弧,δij =1;当Pi不是Tj的输入时,δij = 0,i = 1,2,…,m,j = 1,2,…,n。

3.3 知识推理
采用MYCIN的置信度方法[11]实现知识推理,步骤如下:
(1)由输入信息或知识的置信度确定库所(命题)的初始状态q 0。
(2)由公式
4 基于RST与FPN的变压器故障诊断模型
4.1 RST与FPN的互补性分析
从以上的理论分析可以看出,粗糙集信息表和模糊Petri网络都可以有效表达故障诊断专家系统知识库中启发式规则。粗糙集信息表的优点在于通过约简诊断规则,可以对诊断规则进行压缩,剔除不需要的特征,使诊断规则得到有效简化,提高了故障诊断的效率。但是,当采用粗糙集信息表进行推理时,如果数据量较大,查表搜索规则是一个计算量很大的过程。此外,尽管粗糙集信息表中属性的属性值都是含糊描述的,如正常、超标、下降等,而实际约简时均是当作离散量进行处理的,本质上还是一种定性分析,因此并不适于模糊推理,会出现临界问题,造成分类错误或误判。
在专家系统中利用模糊Petri网络方法表示启发式知识,知识库系统结构简单、规范、空间搜索效率高,易于实现并行模糊推理。但是FPN只有知识表达与推理能力,完全依赖于先验知识,并没有对知识进一步简化的能力,往往先验知识中存在一定的冗余性,将导致网络规模过于庞大,故障特征的获取工作繁重,直接影响推理的效率。例如,表达表1中的规则,需要14个库所和7个变迁,而对于表2中的规则,只需7个库所和4个变迁,但表达能力没有改变。
可见RST与FPN在利用模糊启发式知识进行诊断推理上具有较强的互补性,即利用粗糙集的数据分析、压缩和容错能力,实现对专家知识的简化与故障特征的压缩,获得最小诊断规则,用来建立最优的模糊Petri网络模型;而利用模糊Petri网络处理并行模糊推理的能力来实现高效、快速的故障诊断。这样将粗糙集与模糊Petri网络的功能作了串形结合,可以同时克服粗糙集的规则搜索、临界问题和模糊Petri网络的冗余性问题,利于充分发挥它们各自的优点,也把定性与定量分析结合了起来。
4.2 诊断模型的建立
在搜集有关文献资料基础上给出了具有代表性的变压器故障实例[7-8],这些实例中故障类型与特征的关系如表3所示。从粗糙集理论的观点,表3也是一张信息表,条件属性集为{s1, s2,…, s7},结论属性为故障类型。
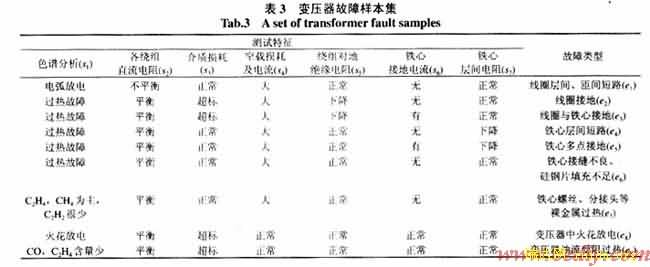
按2.2节中的步骤1、2对表3进行处理,得出最小属性集{s1, s3, s6, s7}和{ s1, s5, s6, s7},两个最小属性集能够完全区分出各种故障,表明故障特征中存在着冗余信息。这就为在不完整特征信息下的变压器故障诊断提供了一条新的思路,即利用故障特征信息的冗余性,选择约简得到不同的属性集,通过避开信号提取困难或受干扰较为强烈的那些特征,从而达到准确诊断的目的。
按步骤3、4、5处理最小属性集{s1, s3, s6, s7}所对应的规则,可得出最小诊断规则,即
由以上规则得出的模糊Petri网络模型结构如图2所示。

相应的输入矩阵与输出矩阵分别为
根据主观经验并搜集相关文献[5]得出置信度矩阵
U = diag (0.85, 0.9, 0.8, 0.9, 1.0, 0.85, 0.9)
5 故障诊断实例
对某变电站主变进行色谱分析,各特征气体的比值结果如下:j(CO)/j(CO2)=0.1、j(CH4)/j(H2)= 2.34、j(C2H2)/ j(C2H4)=0.061、j(C2H4)/ j(C2H6)= 2.11。在进行的电气试验项目中,铁心接地电流为0.135,介质损耗为1.58%,铁心段间电阻为0。
考虑到模糊边界数量级对隶属函数的影响,采用半梯形分布来确定隶属度,由于篇幅所限,请具体参阅规程及文献[5-6]。由给定的测试结果,模糊处理后,可以得出初始状态
其中p11(铁心多点接地)发生的置信度为0.8125,远远大于其它命题的置信度,据此可以推断出发生多点接地故障的可能性最大。对变压器进行吊罩检查,发现B相压环与铁心间通过支持螺丝短路。由于绝缘设计不合理,运行时振动等原因使环氧树脂破损,造成压环与铁心短路,形成多点接地。
6 结论
本文将粗糙集理论与模糊Petri网络有机结合在一起,利用粗糙集信息表简化技术从复杂的油浸电力变压器故障诊断实例中提取最小诊断规则,实现最优模糊Petri网络故障诊断模型的建立。利用模糊Petri网络诊断不仅可有效地进行模糊推理,其并行处理能力能大大减少以往知识库中搜索的步骤,提高了诊断的速度与效率。实例证明,该组合方法能有效地压缩故障特征空间,实现快速、准确的并行模糊推理。此外,该方法为油浸电力变压器故障诊断中实现智能互补进行了有益的尝试。
参考文献
[1] 杜洋(Du Yang).用气相色谱法判断变压器故障诊断的简易方法(Easy methods to determine the characteristic of breakdown according to gas dissolving into oil of transformers)[J].高电压技术(High Voltage Engineering),1995,21(4):61-63.
[2] Kemp I J.Partial discharge plant-monitor technology:present and future developments [J].IEE Pro.-Sci. Maes. Technol.,1995,142(1):4-10.
[3] 应鸿,李天云,陈化钢(Ying Hong,Li Tianyun,Chen Huagang).用神经网络方法诊断变压器故障(Transformer fault diagnosis by artificial neural network method)[J].变压器(Transformer),1997, 34(9):22-25.
[4] 王大忠,徐文,周泽存(Wang Dazhong,Xu Wen,Zhou Zecun).模糊理论、专家系统及人工神经网络在变压器故障诊断中的应用-基于油中溶解气体进行分析诊断(Application of fuzzy sets theory, expert system and artificial neural networks in faults diagnosis of power transformer)[J].中国电机工程学报(Proceedings of the CSEE), 1996,16(5):349-353.
[5] 杨莉,尚勇,周跃峰,等(Yang Li,Shang Yong, Zhou Yuefeng,et al).基于概率推理和模糊数学的变压器综合故障诊断模型(Probability reasoning and fuzzy technique applied for identifying power transformer malfunction)[J].中国电机工程学报(Proceedings of the CSEE),2000,20(7):19-23.
[6] 金松茂,江汉荣(Jin Songmao,Jiang Hanrong).证据结合在电力设备故障诊断中的应用(Application of evidence combination to fault diagnosis of electric power transformer)[J].湖南大学学报(自然科学版)(Journal of Hunan University (Natural Sciences Edition)),2001,28 (2):55-60.
[7] 孙辉,李卫东,孙启忠(Sun Hui,Li Weidong,Sun Qizhong).判决树方法用于变压器故障诊断的研究(Electric power transformer fault diagnosis using decision tree)[J].中国电机工程学报(Proceedings of the CSEE),2001,21(2):50-55.
[8] 王建元,纪延超(Wang Jianyuan,Ji Yanchao).模糊Petri网络知识表示方法及其在变压器故障诊断中的应用(Application of fuzzy petri nets knowledge representation in electric power transformer fault diagnosis)[J].中国电机工程学报(Proceedings of the CSEE),2003, 23(1):121-125.
[9] 杜海峰,王孙安,丁国锋(Du Haifeng,Wang Sunan,Ding Guofeng).基于粗糙集与神经网络的多级压缩机诊断(Fault diagnosis of the reciprocating compressor based on integrated rough sets and fuzzy neural network)[J].西安交通大学学报(Journal of Xi’an Jiaotong University),2000,35(9):940-944.
[10] 高梅梅,吴智铭(Gao Meimei,Wu Zhiming).模糊Petri网络及其在故障诊断中的应用(Fuzzy reasoning petri net and its application to fault diagnosis)[J].自动化学报(Acta Automatica Sinica),2000,9(26):677-680.
[11] 杨叔子.基于知识的诊断推理[M]. 北京: 清华大学出版社,1993.