电流环控制的降压PWM开关电源系统的建模分析

摘要：PWM开关电源系统普遍采用电流、电压双闭环控制。在建立PWM降压开关电源功率级模型的基础上，得出基于平均电流控制的降压PWM开关电源的系统传递函数框图，并用Matlab对电流环增益进行了分析。

随着便携式电子设备产品的发展，PWMDC－DC开关电源获得了广泛应用。在系统的功率级电路中，主开关和辅助开关呈现非线性特性，给系统建模增加了难度，但系统中除主开关和辅助开关外，其余部分均是线性电路。因此，系统分析的关键在功率级模型的建立。
　　本文从PWM降压开关电源的拓扑结构和功率开关的线性等效电路入手，研究功率级的传递函数，再与控制电路的模型相结合，提出了整个系统的框图结构，它适于采用双闭环控制的PWM开关电源系统。通过应用Matlab分析一个基于平均电流控制的PWM降压开关电源系统的实例，这些传递函数的准确性得到验证。

1　功率开关的线性等效电路　　
图1给出了PWM降压开关电源系统的拓扑图，其中r_c为滤波电容C的寄生电阻。从三端网络的观点考察其中的PWM功率开关^［1］：a端为主开关；p端为辅助开关，即整流管；c端为两管的公共端。文献［1］给出网络各端口的电流电压与系统的稳态分量和瞬态分量之间的相互关系式为：

式中D表示系统稳定状态下的占空比，d为D的扰动量；各大写电压、电流符号表示稳态分量，小写电压、电流符号表示瞬态分量。由此导出开关级的线性等效电路如图2。

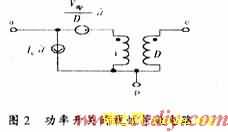
2　降压开关电源的功率级的模型　　
　　将开关级的线性等效电路嵌入PWM降压开关电源拓扑图中，得图3（a）所示等效电路。很明显，负载电压v₀和电感电流i_L同时受输入电压v_g和占空比扰动d的调节。欲分析功率级的工作状况，首先需要考虑各种因素独立作用的影响，即必须先求出以下四个传递函数^［2］：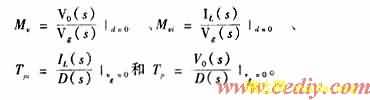

    1）　稳态直流分析

　　2）　求M_v
令d＝0，得图3（c）。由V_cp（s）＝DV_g（s）及次级侧的分压关系，列得：

3）求Mri
    由图3（c），根据次级侧回路电压方程，有：
    I_L(s).{LsR_L//}[rc+(1/Cs)]=DV_g(s) (5)

4）　求T_pi
如图3（d），在次级侧，有：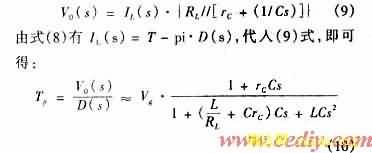

　　式（4）、（6）、（8）、（10）即为PWM降压开关电压系统的功率级的主要传递函数。应用叠加原理，并考虑v₀和v_g对占空比的前馈影响因子G_O、G_G^［3］，可建立功率级的传递函数框图。
3　系统实例分析　　
　　采用平均电流控制的PWM降压开关电源系统结构如图4。控制电路包含两个负反馈环路：内环为由电流检测放大器、电流调节器、占空比调制器和功率级组成的电流控制环；外环则是包含了电阻分压器、误差放大器、电流调节器、占空比调制器和功率级的电压控制环。本文综合控制电路复频域模型^［3，4］（详见附录1），提出基于平均电流控制的PWM降压开关电源系统的完整的模型如图5。

电流环环路增益T₁（s）定义为在复频域中，当电压环开路时，电流环的开环增益。因为采用双闭环控制，系统存在稳定性问题^[5]，所以分析T₁(s)对设定电流调节器的电路参数、以及综合平衡系统的稳定性和快速性有重要意义。
由图5断开电压负反馈环，算得电流环环路增益参照文献［3］提供的电路参数值，通过Matlab模型画出T_I（s）的Bode图如图6所示。为验证本文提出的模型的准确性，文献［3］的理论结果也在图6中给出。
4　结　论　　
　　本模型能准确反映电流环环路增益的低频增益、截止频率和相位裕度。因为考虑了r_c的影响，本文的结果更逼近实际情况。另外，由于功率级模型也采用了框图形式，各环节与实际电路结构对应更为明确，有利于系统的分析与设计。
　　若移除图4中的电流调节器，令图5电流环中的G_CL（s）＝1，并去掉电压环中的1＋G_CL（s）环节，可得到采用峰值电流控制的PWM降压开关电源系统的框图。
　　准确的数学模型是进行系统分析与设计的必要工具，利用本模型和Matlab软件可以很方便地对系统进行分析、设计与调试。
　　附录1　控制电路各环节传递函数^［3，4］

参考文献

［1］　Vatche Vorperian．Simplified Analysis of PWM ConvertersUsing Model of PWM Switch Part I：Continuous ConductionMode［J］．IEEE Transactions on Aerospace and electronic　systems，1990，26（3）：490－496．
［2］　Marian K．Kazimierczuk．Transfer Function of Current Modu－lator in PWM Converters with Current－Mode Control［J］．IEEEtransactions on circuits and systems，2000，47（9）：1407－1412．
［3］　Philip Cooke．Modeling Average Current Mode Control［J］．IEEE2000：256－262．
［4］　Wei Tang；Fred C．Lee and Raymond B．Ridley．Small－Sig－nal Modeling of Average Current－Mode Control［J］．IEEE　Transactions on power electronics，1993，8（2）：112－119．
［5］　Tse CKand Lai Y M．Controlof Bifurcation in Current－Pro－grammed DC／DCConverters：A Reexamination of Slop Com－pensation［C］．In：IEEEInternationalsymposiumon circuitsand systems，geneva Switzerland 2000：I－671－I－674．