逻辑代数的化简算法

观察函数

1.该函数有四个逻辑变量，可表示成

Y=f(A、B、C、D)

2.该函数有三个乘积项：第一项有四个因子——四个变量在乘积项中都出现了。第二项有三个因子——缺少变量B（或）。第三项缺少变量C、D（或、）。

3.第一个乘积项是A、B、C、D的一个最小项，其余二项均不是A、B、C、D的最小项。

最小项：n个逻辑变量A1、A2、…… An组成的逻辑系统中含n个因子的乘积项——每个变量（或）在乘积项中只出现一次，称这样的乘积项为最小项。

两个逻辑变量A、B有22＝4个最小项，分别是：、、、。

三个逻辑变量A、B、C有23＝8个最小项，分别是：、、、、、、、。

四个逻辑变量A、B、C、D有24＝16个最小项。

练习：写出A、B、C、D的十六个最小项。

最小项的性质：

（1）对变量的任意一组取值，只有一个最小项为1，其余最小项全为0。二变量A、B的最小项为：、、、。对A、B的任意一组取值：

A=0 B=0 =1 其余三项全为0，即＝＝＝0

A=0 B=1 = 1 其余三项全为0

A=1 B=0 = 1 其余三项全为0

A=1 B=1 = 1 其余三项全为0

（2）全体最小项之和为1。（读者自己证明）

（3）任意两个最小项的乘积为0。

最小项的编号：

三变量A、B、C的八组取值000、001、……111能分别使八个最小项的值为1，又与十进制数0，1……7的二进制数表示相同。用0～7编号八个最小项，记为：m0、m1、m2、m3、m4、m5、m6、m7，则m7＝m111＝，……m4＝m100＝，m0＝m000＝。

练习：读者试写出四变量A、B、C、D的十六个最小项m0、m1……m15。

逻辑函数的最小项之和形式

任何逻辑函数都可化为最小项之和的标准形式

例：将下列函数化为最小项之和的形式

反函数的最小项之和表示

例：求二变量A，B的逻辑函数的反函数。

解一：

解二：列真值表

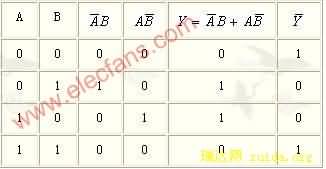
由真值表写出的逻辑表达式

(全体最小项之和)

如三变量A,B,C的逻辑函数则必有

结论：在n个变量的逻辑系统中，如果Y为i个最小项之和，则必为余下的（n－i）个最小项之和。

异或运算与同或运算

定义： 称A与B异或，为异或运算符

A与B同或，为同或运算符

显然：

异或与同或互为反函数

由此推得：

即两者相等为0，不相等为1

同或运算则与之相反，且有

同学自己证明并牢记。

例1． 将下列函数化为最简与或式。

例2． A，B的波形如下图所示,试画出的波形。

最小项的相邻性

任何两个最小项如果他们只有一个因子不同，其余因子都相同，则称这两个最小项为相邻最小项。

显然，m0与m1具有相邻性，而与不相邻，因为他们有两个因子不相同。m3与m4也不相邻，而m3与m2相邻。

相邻的两个最小项之和可以合并成一项，并消去一个变量。如：

卡诺图

卡诺图是美国工程师卡诺（Karnaugh）发明的。用小方块（格）来表示最小项。三变量的卡诺图画八个小方块（格）来表示八个最小项，四变量的卡诺图画十六个小方块来表示十六个最小项。……

观察三变量卡诺图发现这八个小方块（最小项）中，凡几何上相邻的两个小方块（最小项）具有相邻性――只有一个变量不同，相加后能合并成一项，并能消去一个变量。

m0m1 ，m1m3 ，m3m2 ，m4m5 ，m5m7 ，m7m6 ， m0m4 ，m1m5 ，m3m7 ，m2m6都具有相邻性，还有m0m2 ，m1m6也具有相邻性（可理解成将卡诺图卷成圆筒，他们在几何上就相邻了）。

在四变量卡诺图中，m0m8 ,m1m9 ,m3m11 ,m2m6也都具有相邻性。

思考题：为什么卡诺图按00，01，11，10的顺序，而非00，01，10，11顺序画小方块（代表最小项）？

逻辑函数的卡诺图表示及化简

在逻辑函数的最小项表示一节中，已经讲过，任何一个逻辑函数都可以化为最小项之和的标准形式。

只要将标准形式里函数所包含的每一个最小项，在卡诺图中对应的小方块里添上1，卡诺图上其余的小方块里添0（以后添0，以空格代替）――这就是逻辑函数的卡诺图。

其实将函数化为最小项之和，再画卡诺图的过程可以简化，函数化为最小项之和的过程可以省略，直接画出卡诺图。

例1． 画出的卡诺图并化简

解：1、画出Y的卡诺图

Y共有四个乘积项，第一个乘积项包含第4行的四项：m8，m9，m11，m10；第二个乘积项包含第1，2行（A＝0）与第3，4列（C＝1）相交的四项：m3，m2，m7，m6 ；第三个乘积项包含第2，3行（B＝1）与第3，4列（C＝1）相交的四项：m7，m6，m15，m14；第四个乘积项表第2列的4项。

2、合并与化简

从Y的卡诺图上看到第2，3列8项合并，第3，4列8项合并，第4行合并得：

例2．

解：1、画出Y的卡诺图

第1项，显然第4行中的4个最小项都含因子，而第1，2列的8个最小项都含因子，第4列与第1，2列相交的两项m8，m9即为。第4项C则包含第3，4两列的8项。

2、合并化简。从卡诺图可知

用卡诺图化简逻辑函数小结：

1． 画出逻辑函数的卡诺图。

2． 若两个最小项相邻， 则可合并为一项，且消去一个因子。

3． 若四个最小项相邻（排列成一个矩形组），则该四个最小项可合并成一项，且可消去两个因子。

4． 若八个最小项相邻（排列成一个矩形组），则该八个最小项可合并成一项，且可消去三个因子。

5. 若十六个最小项相邻（排列成一个矩形组），则该十六个最小项可合并成一项，且可消去四个因子。

无关项在逻辑函数化简中的应用

我们来分析一个实际问题：

某水库设有三个水位检测点，装有A、B、C三个干湿传感

器，当传感器被水浸泡时输出1，否则（不浸水时）输出0。该水库有大小两个闸门GL、GS。A为警戒水位点，B比警戒水位A高1米，C比警戒水位高2米。防汛部规定当水位低于警戒水位A时，关闸蓄水。当水位超过A时，开小闸门GS放水，当水位超过B时，开启大闸门GL（关闭小闸门）泄洪；当水位超过C时，大小闸门ＧLＧS同时开启泄洪。如果用1表示闸门关闭，闸门与水库水位之间的逻辑关系真值表如下：

说明：水位低于警戒线，关闸蓄水

水位超警戒线，只开小闸门放水

只开大闸门泄洪

大小闸门同时泄洪

从前面讲过的内容来看GL=AB，这两个逻辑函数已经不能再化简了，但从现实角度看应该有更简化的结果GL=B，因为只要水位超过B（B＝1），大闸门就要开启，与是否超过C无关（因为C＝1时，B也等于1），同样。

这就是说明前面讲过的内容还有欠缺的地方。

我们观察上面的真值表发现，A、B、C三个代表水位的逻辑变量，可能的取值只有000、100、110和111四种。其余四种取值001、010、011和101永远不可能出现。因为没有物理意义。如果001，C＝1，A＝B＝0这是不可能的。

自己证A、B、C永远不可能取001、010、011和101。与之对应的四个最小项就永远为0。m1=0，m2=2，m3=0，m5=0或。

初等函数有定义域Y＝，不允许X取（－1，3）之间的数，逻辑函数也有类似的问题。上面讲的水位检测问题A、B、C的取值只有000、100、110、111四种情况，001、010、011和101无意义，永远不可能出现，与之对应的四个最小项将永远为0，即。这就是下面要讲的无关项问题。

无关项

由于逻辑变量的取值受到限制（约束），使得某些最小项（及其和）永远等于0，那些恒等于0的最小项就是无关项。

在卡诺图中无关项用x表示。如对化简逻辑函数有用，对组成更大的相邻矩形组有用，可将他们吸收进去（因为他们为0，等于在逻辑函数中添加0）反之弃之。

例：将下列函数化为最简与或函数式。

给定约束条件 AB+CD=0

约束条件

解：

    .该卡诺图上有四个矩形组
,其中m11，m13，m15三个无关项在化简中没有用到。