摘  要：分析了高压倍压整流电路在中高频条件下无功功率产生的原因，以减小供电逆变器容量为目的，提出了具体的功率因数补偿方法，并通过实验证明了有效性。

关键词：多级倍压整流，高压，无功补偿

The Correction Method of Reactive Power in Cockcroft-Walton Voltage Multiplier

Li Dongcang, Yang Lei, Ding Guangze

(Lanzhou University, Lanzhou, 730000)

Abstract: This paper analyzed the reason that the Cockcroft-Walton voltage multiplier produced the reactive power in the condition of high frequency. For the purpose of reducing the capability of supply inverter, the method of power factor correction is present, and proved its validity by the experiment.

Key words: Cockcroft-Walton voltage multiplier  high-voltage  reactive power correction

1  引  言

在电能的利用中，供电电压与负载电流的相位通常是不一致的，这种相位差就产生了无功功率。负载是感性负载时，电流相位滞后电压相位，这是普遍存在的，为此，发展了各种无源和有源的无功补偿方法和技术，以期提高功率因数；而当负载为容性负载时，也会产生无功功率，当电容量足够大或工作频率足够高时，容性无功功率就不容忽视了。本文将要讨论的正是后一种情况。在直流高电压的产生方式中，多级倍压整流电路是应用最多的方式之一，它的高电压，大输出电流及易实现性是其主要优点。高的工作频率，小的滤波电容和少的倍压级数是所希望的。但是，由于升压变压器的大变比、寄生电容以及倍压整流滤波电容的存在，使得多级倍压整流电路呈现容性负载。对小功率高压直流电源而言，可通过增大供电逆变器电源的容量来解决，但在中大功率高压输出时，上述措施就显得力不从心和得不偿失，为此，通过分析倍压整流电路和升压变压器的工作原理，得到电路的等效模型，利用电工学原理，提出了解决对策，并成功地应用于一台高压直流电源上。

2  倍压整流电路等效容抗

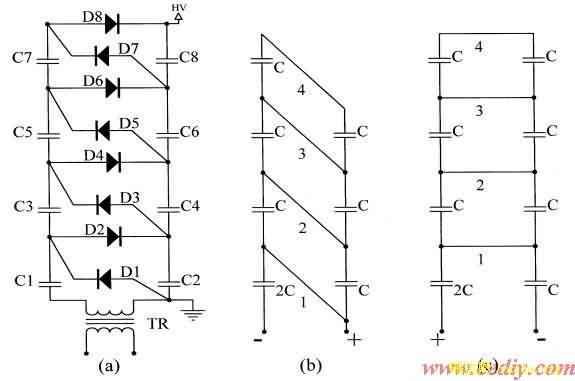
一个四级倍压整流电路如图1a所示，电容C1为2C，C2~C8为C，D1~D8为高压整流硅堆，为理想二极管，TR为升压变压器，C1，C3，C5，C7构成交流电容柱，C2，C4，C6，C8构成直流电容柱，空载输出高压UH为：

UH=2NU2P-P                                   （1）

其中N为倍压级数，U2P-P为升压变压器次级电压峰值。

倍压整流电路工作时，对电容的充电分两个阶段。在输入交流的正半周，充电是对交流电容柱进行的，如图1b所示，充电回路由1~4个支路并联而成。所以，在正半周时，等效电容就是四个支路的电容的并联：

              （2）

                    （3）

在输入交流的负半周，充电是对直流电容柱进行的，如图1c所示，充电回路也由4个支路并联而成，所以，在负半周时，等效电容为：

            （4）

                   （5）

正负半周的等效电容估算出来，但等效容抗的大小还与充电时间有关，在倍压整流电路中，电容的充电不是全波充电，而是以脉冲进行充电，只有在时间D内，变压器的次级电压对电容充电，D之外，电容没有充电电流，所以，在计算等效容抗时，只计及D内的效应，也就是说，应加入占空比D（D<1）因子：

                         （6）

其中： 为工作频率，C为单位电容量，D为占空比。占空比D还与高压负载电流大小有关，是一变化的量，当高压负载电流为额定值时，D约为5%~10%。

3  升压变压器寄生电容容抗

升压变压器具有较大的变比和较多的次级绕组匝数，绕组的层与层之间有寄生电容，每一层的匝与匝之间亦有寄生电容。在低频供电的条件下，由寄生电容引起的无功功率很小，可忽略不计。但当频率从50Hz提高到2.5kHz以至20kHz时，产生的无功功率就相当可观了。变压器寄生电容的理论计算受许多条件的限制而不准确，通过实验方法测量是简便和可行的。举例说明：实验中所采用的变压器铁芯为微晶合金环型铁芯，初级绕组N1=21匝，次级绕组N2=2400匝，采用分段绕法，分四段，以减小寄生电容，变比B=114，工作频率f=15kHz，变压器的次级不接任何负载，初级加中频电压Ui(V),测量中频电流Ii(A),即可计算出等效容抗：

                      （7）

其中：N为测量次数，XC1为初级等效容抗，可以继续算出次级等效容抗XC2和寄生电容量C2：

                      （8）

                          （9）

说明：在计算容抗时没有计及升压变压器初级励磁电流分量，是因为该电流很小，略去不计不会影响测量精度。

4  无功功率补偿策略

通过以上分析可知，高压倍压整流电路是一容性负载，容性负载的无功补偿采用电感，针对这一特定负载的模型，有三种补偿对策可供选择：在升压变压器初级补偿，将倍压整流电路和升压变压器的等效容抗全部包含在内；在升压变压器次级补偿，只能对倍压整流电路的无功功率进行补偿，对升压变压器寄生电容的无功功率无能为力；前后综合补偿，即同时采用前面两种方法。通过分析可知，只有第一种对策是可行的。

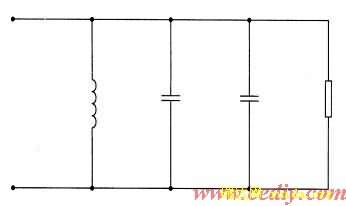
补偿等效电路如图2a所示，XC1为变压器寄生电容容抗，XC2倍压整流电路等效容抗，RH为高压负载等效电阻，XL为补偿电感感抗，该电感为空心电抗器。图2b为补偿矢量图，I1为补偿前电流，I为补偿后电流，如果为适当补偿时，I和IH相等。

4  实验条件与结果

该直流高压电源设计为4级倍压整流，升压变压器变比为114，空载最高输出电压为直流250kV，在200kV时额定负载电流为10mA。在高压电源只有测量电阻(890M )和加速管均压电阻（192M ）的轻载（高压200kV时高压负载电流为1.2mA）条件下，对补偿和未补偿进行了对比实验测试，逆变电源输出电压和负载电流的关系如图3a所示，补偿电感L=225 H；在加速器引出束流的负载（高压200kV时高压负载电流为4.5mA）条件下，对补偿和未补偿进行了对比实验测试，逆变电源输出电压和负载电流的关系如图3b所示。可以看出补偿后使负载电流有效值降为补偿前50%左右，大大减轻了中频逆变电源的负担，证明了该补偿的有效性。

当然，存在的问题是，由于高压负载的变化，使占空比D有所变化，所以倍压整流电路等效容抗会有改变，而补偿电感是固定的，会使补偿效果不如预期的好，但也得到了较好的结果，为解决这个问题，可考虑采用有级可调电感。

参考文献：

[1]  桂伟爕  荷电粒子加速器原理  清华大学出版社，1994年。

[2]  秦曾煌  电工学（上册）  高等教育出版社，1999年。