 打印本文
打印本文  关闭窗口
关闭窗口 关键词:ANSYS软件包 仿真 稳态热阻
The Simulation on Stable-state Thermal Resistance of
Sinks for Power Semiconductor Devices Using the ANSYS Software
ZHANG Fa-sheng1 HE Duo-chang2
(1.College of Electronic Information of Central South Forestry University,Zhuzhou 412006 ,China );
(2. Zhuzhou Electric Locomotive Research Institute,Ministry of Railways,Zhuzhou 412001 ,China )
Abstract:This paper discusses the theoretical analysis of the stable-state thermal resistance of sinks for power semiconductor devices using the ANSYS multi-physical field and simulates the Stable-state Thermal Resistance of the copper-Sinks for SS7D。A set of simulated results is in good agreement with experimental data ,so the method is proved to be correct。
Key words:ANSYS software Simulation stable-state thermal resistance
1 引 言
功率半导体器件是高发热的电器产品,功率半导体器件的结温高低直接关系到器件的工作状态和承受浪涌电流的能力[1]。功率半导体器件的结温一方面取决于器件损耗的大小,另一方面取决于这些损耗被带走的速度,即取决于散热冷却条件。功率半导体器件用的散热器的目的是控制半导体器件的结温Tj ,使其低于半导体器件的最大结温Tjmax ,从而提高半导体器件的稳定性和可靠性。因此,深入而准确地了解功率半导体器件用散热器的温度场分布,对于功率半导体器件的应用,无疑是一个十分重要的基本问题。温度场的仿真计算及分析,是世界各种优化设计其产品的一种重要手段,大到一艘潜艇,一架飞机,小到一台PC机机箱,一块冷却板均应用这一技术进行优化设计。在机车上,因此体积,重量受到严格限制,加上其电气发热密度大,因此通风冷却是机车关键设计技术之一。在我国机车通风冷却设计技术中,还没有或很少利用计算机进行仿真计算,优化,一般还是根据经验进行,设计较粗糙,不能满足生产实验的需要,必须对功率半导体器件用的散热器进行仿真计算,达到优化设计的目的。而ANSYS多物理场软件包恰恰可以对温度场,流场等方面内容进行仿真。因此,本文介绍用ANSYS多物理场软件包对功率半导体器件用散热器进行温度场仿真计算,且计算结果与测试结果吻合得很好。
2 理论分析
根据传热学模拟理论,不论是什么样的散热器模型都必须按照通一的原则加以分析和研究,即求解导热微分方程。我们知道,在传热学中,具有内热源和瞬态温度场的三维导热在直角坐标系中的微分方程式为[2]: t / τ=λ/ ρc ( 2t/ x2+ 2t/ y2+ 2t/ z2+θ/λ) ………… (1)
式中:t:为物体的瞬态温度
τ:为时间
ρ:密度
c:为比热容
λ:为导热率
θ:为单位体积内热源的生成热
求解上述导热问题,实质上归结为对导热微分方程式的求解。为了使微分方程得到唯一解,还必须给出边界条件和初始条件。
(Ⅰ) 规定了边界上的温度值,称为第一类边界条件,用公式描述为:
Tw = f1 ( x ,y ,z ,τ) ……… (2)
(Ⅱ) 规定了边界上的电流密度值,称为第二类边界条件,用公式描述为:
—λ( t/ n)w = f2 ( x ,y ,z ,τ ) ……… (3)
式中:n为表面的法线方向。
(Ⅲ) 规定了边界上物体与周围流体间的换热系数a及周围流体的温度tf ,称为第三类边界条件。用公式描述为 :
—λ( t/ n)w = a( tw—tf ) ………… (4)
按照有限元法的理论[3],将原始方程变换成积分形式,它是基于求一个量的最小值将导致真实解的概念。变分原理的等价定理指出,求解原始微分方程等价于求下式定义的泛函Ie (T)的最小值[4]。即使
Ie(Ti)/ Ti=∫∫∫ { ax· 2t/ x2 + ay· 2t/ y2 + az· 2t/ z2 +
△R
( t/ τ- θ/ τ)}dxdydz +∫∫ (λ/ρc) t/ n·ds = 0 ………… (5)
△C
式中△R是单元所包含的子域,△C是在表面C上的面积,显然只有靠近边界C的单元才会出现这一项。(5)式对于所有网格点i成立,便构成一个联立方程系统,求解这个系统可得到整个问题的数值解,即温度场分布。
3 ANSYS软件稳态热分析的基本过程
ANSYS软件包仿真热分析的基本过程包括三个步骤:
第一步骤为前处理,其任务是建模。首先确定文件名、分析标题、单位,然后确定软件单元类型、实常数、材料热性能参数,最后创建几何模型并划分网格。
第二步骤为加载计算。在这一过程中,首先确定文件分析类型,然后对该模型施加载荷,最后对该模型进行求解。
第三步骤为后处理,其作用是查看结果。在这一过程中,ANSYS软件可用后处理软件查看由上一步计算好的数据。
4 结果与验证
本次我们仿真的对象为韶山7型(SS7D)电力机车主整流器功率半导体器件用散热器。由前面的分析可知,ANSYS软件包对热场的分析是基于有限元计算,若有限元分析计算量很大,轻则耗用的计算时间长,重则计算机无法正常工作。为此,在保证精度的情况下,对所模拟的散热器模型进行简化,是非常必要的。因此,我们结合韶山SS7D机车主整流器功率半导体器件用散热器的结构形状对称性,所选模拟模型为实际结构整体的1/4(如图1所示)。图2和图3分别是韶山SS7D用散热器在被施加1393W和1979W功率时,所得到的数值仿真温度场分布图。通过分析计算、对比,证明了数值仿真结果与测试结果非常接近。但毕竟试验结果与仿真结果有细微的偏差,这个偏差主要来源于两个方面, 一个方面是由于试验测试的仪器(主要是热电偶)的误差,另一方面是由于ANSYS软件包允许剖分网格总数量的限制,致使仿真的结果与实际数值也会造成细小的误差。
散热器测试结果与仿真结果如下表:
研究方法 | 散热器 | 电流(A) | 压降(V) | 台面平均 | 平均风温 | 风速(m/s) | 温升(0C) | 耗 散 | 稳 态 |
实验测试1 | SS7D | 12.5 | 111.5 | 75.5 | 42.0 | 5.9 | 33.5 | 1393 | 0.024 |
实验测试2 | SS7D | 14.5 | 136.5 | 93.0 | 43.5 | 5.9 | 49.5 | 1976 | 0.025 |
数值仿真1 | SS7D | 12.5 | 111.5 | 78.0 | 42.0 | 5.9 | 36.0 | 1393 | 0.0258 |
数值仿真2 | SS7D | 14.5 | 136.5 | 93.0 | 42.0 | 5.9 | 51.0 | 1976 | 0.0258 |
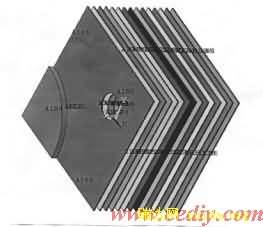
图1 为SS7D机车主整流器功率半导体器件用的铜散热器模型(仅为整体1/4)
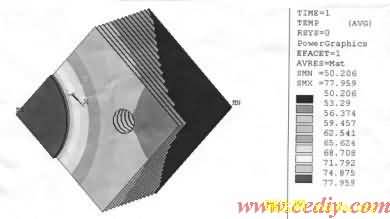
图2 为SS7D用散热器在被施加1393W功率时,得到的仿真温度场分布图
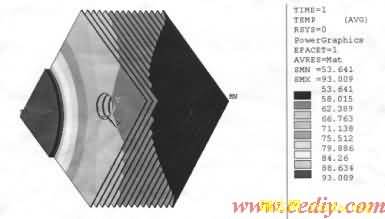
图3 为SS7D用散热器在被施加1979W功率时,得到的仿真温度场分布图
5 结 论
纵上所述,我们已经基本上掌握了利用ANSYS多物理场软件包仿真散热器的温度场分布的技术。该技术的关键在于根据变流技术电路中功率器件实际耗散功率的大小并结合本软件允许剖分网格点数量(该网格点数量一般为3~4万个网格)的限制,建立合理的几何模型和划分网格的精细程度,就可以得到比较满意的仿真结果。目前我们在设计功率半导体器件用的散热器时,首先就必须利用ANSYS软件包进行仿真,并根据仿真的优化结果来设计具体的散热器,这不仅效果好,而且节约大量的前期试验时间和研究费用,这将为散热器的优化设计提供了一个重要手段。
参考文献:
[1] 陈治明等,“6000V晶闸管正向压降的计算机模拟”,半导体学报,第五期(1990.5)
[2] 杨世铭,传热学,高等教育出版社,1987,第二章。
[3] T.Adachietal,IEEE Trans.,ED—26(7),PP.1026 ~131,1979。
[4] 朱伯芳,有限单元法原理与应用,水利电力出版社,1979,第四章。
[基金项目] 铁道部株洲电力机车研究所所级研究课题的内容
作者简介:
张发生(1965-) 男, 江西临川人,硕士, 副教授 , 现从事电力电子技术教学研究工作。
 打印本文
打印本文  关闭窗口
关闭窗口