1 引言
    Bergen和Hill首先提出了网络结构保持模型^[1]（Network Structure Preserving Model），随后文[2]、[3]又分别在此基础上做了改进。由于建模考虑了网络结构，涉及到负荷节点，使得模型中引入了潮流约束方程。 这样，结构保持模型被表示成一组微分代数方程DAE。该模型虽然能更加准确地描述电力系统，但将传统的稳定性判定方法应用于其上时却出现了较大的困难。
    将传统Controlling UEP推广至结构保持模型，除EEAC方法^[4]本身所具有的特点使其不受DAE影响之外，文[5]~[13]分别利用局部分析方法及奇异摄动方法还做出了许多卓有成效的工作。其中，局部分析方法虽然理论上很完备，但由于奇异面的存在而不能获得全局的结论，而且每个代数子流形都对应于不同的ODE，使得它难以应用。奇异摄动方法,即所谓的边界层方程BLE，通过它可得到对应于DAE的BLE。在某些范围内，BLE可以近似地表示DAE的动态特性，而且对基于BLE的电力系统模型运用Controlling UEP方法能够保证持续故障轨迹与故障后系统稳定域边界相撞。虽然将DAE转化为BLE可以获得全局结论，但这并没有得到证明，况且并非任何情况下DAE都可以等价的转化为BLE。
    由上可见，Controlling UEP应用于结构保持模型较经典模型要困难得多，而且准确的负荷建模一直是个难题^[14]。文[15]的理论分析部分已经讨论了结构保持模型中的奇异性质以及传统Controlling UEP理论应用于该模型的难点，并就此对外部跳变行为和故障后DAE系统的稳定性进行了分析。在此基础上，本文将提出基于结构保持模型的稳定性判定方法。
2  现有方法概述及问题
    由于代数流形的约束、跳变行为的存在等原因，使得传统的直接法难以应用于结构保持模型中。文[5]~[13]从两方面提出了解决方法，其分别是应用隐函数定理将DAE在代数流形上等价转化为ODE，本文称之为局部分析方法；另一种是应用奇异摄动方法，将DAE转化为BLE，本文称之为奇异摄动方法。这两种方法的共同目标是相同的，即将DAE化为传统的Controlling UEP能够应用的一组常微分方程。但它们分别存在各自的缺点。
    对于局部分析方法，主要存在以下问题：
    （1） 不能提出全局的结论^[5,16]；
    （2） 没有考虑外部跳变行为。
    虽然存在以上问题，但局部分析方法在确定代数子流形上是准确的，理论上也是完备的。
    S. Sastry等^[12,17]首先将奇异摄动方法引入结构保持模型，随后^[7,9~11,13]都在该方面做了深入的研究。对于奇异摄动方法，主要存在以下问题：
    （1）DAE不能在任何情况下都等价地转化为BLE。
    （2）摄动参数e 的符号确定。同样的e®0，但e <0和e <0对应的BLE轨迹完全不同。文中符号选择的原则是保证BLE与原DAE系统对应的平衡点具有相同稳定属性。
    （3）对于相同的持续故障轨迹，不同的e可能使Controlling UEP不同。那么当e®0时，Controlling UEP是否趋于同一个。
    文[7]、[9]建议通过奇异摄动方法将DAE系统和能量函数方法联系起来，从而获得一个全局的结论。而且BLE存在与e >0无关的能量函数容易构造^[7,9]。但因BLE系统并不和DAE系统等价，它们的轨迹在某些时候也不尽相同，现有判定方法的获得仍需通过启发式的推导。
3  扩展Controlling UEP(ECUEP)方法
3.1 方法提出
    为了克服上述方法存在的问题并结合它们的优点, 本节将在文[15]中定理3的基础上提出新的暂态稳定判定方法，并给出仿真算例。
    定义1  BLE系统是以ODE形式表示的，给定e >0, 通过持续故障轨迹F_f(t) 都能唯一地得到Controlling UEP，记为为方便起见，将其称作F_f(t)的e-Controlling UEP。
    引理1  F_f(t)为给定的持续故障轨迹，初值F_f(t_f)ÎD₀。当故障持续发展时，则存在：

    定义2  F_f(t)为持续故障轨迹，初值F_f(t_f)ÎD₀。若存在序列e_k®0⁺，使F_f(t)主导的e-Controlling UEP都对应于同一个UEP，则称该UEP为不变Controlling UEP。

    引理2  F_f(t)为持续故障轨迹，初值F_f(t_f) ÎD₀。若BLE的稳定域是局部严格等度连续，则不变Controlling UEP是唯一的。
    证明：由定义2及定义3可直接推出该引理。

    其证明参见附录B。


    其证明见附录C。
    虽然本文的讨论未涉及奇异面，但奇异面对暂态过程的影响是非常重要和复杂的^[5,6,16]。上述定理对暂态过程中由奇异面主导的电压失稳不能做出判定，因此, 为排除实际判定中奇异面的影响，可以通过计算代数方程雅克比矩阵的条件数方法来判定系统轨迹是否靠近奇异面，或运用文[16]提出的势能方法（Potential Energy Method）。下面，给出基于结构保持模型的ECUEP方法。
    扩展Controlling UEP方法（ECUEP）：设BLE系统的稳定域是局部严格等度连续的。
    （1）临界能量的确定步骤

    DAE系统的能量函数E_DAE(·)一般很难构造。因此在这里，它可以由能量函数E(·)作合理的替代。
    （2）稳定性判定步骤
    1）使用给定的持续故障轨迹和虚拟持续故障跳变轨迹, 计算故障清除时刻的能量函数值E(·)、E_DAE(·)。

3.2  仿真算例
    考虑如图1所示的单机－两母线系统^[18]。系统的DAE模型如式(3)所示。其中,p₃=2,q₃=1。由于系统较为简单，由式(3)可以求得系统SEP附近的代数流形、UEP及死巷点（这些是本文所关心的），见图2。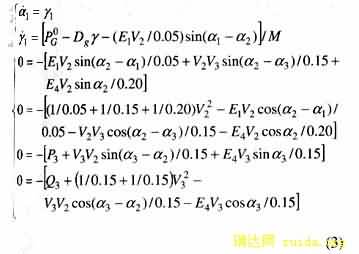

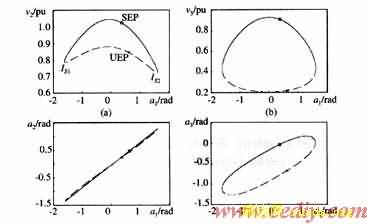
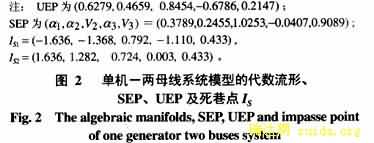
    例1  对图1所示系统，考虑母线B₂三相短路故障，且故障后系统与原系统保持一致。对于给定的故障及实际故障轨迹末值，根据ECUEP方法，判断系统的暂态稳定性步骤如下：
   （1）求取对应于BLE系统及DAE系统的Controlling UEP
    1） 求取BLE系统的Controlling UEP。
　　求取Controlling UEP一直是相关不稳定平衡点方法应用的障碍，BCU方法^[7,19]的提出使得这一问题得以较快速准确地解决。本文运用BCU方法解得BLE系统的Controlling UEP为(0.6279,0.4659,0.8454, -0.6786,0.2147)
    注1  运用文[7]给出的概念性结构保持BCU方法（Conceptual Network-Preserving BCU Method）及文[19]给出的方法计算Controlling UEP，当给定的e 很小时，BLE系统在数值上具有较强的病态特性，由持续故障轨迹从系统稳定域边界上的逸出点作为初值对故障后的降维系统进行积分，所得到的降维系统轨迹迅速趋于L_h附近，只有很弱的靠近Controlling UEP的趋势，如图3。如果将e 取大些，则故障后降维系统的轨迹在某一时刻较为趋于某UEP，如图4。而且随着e的增大，趋近程度越来越大，这样根据文[7]、[19]给出的方法，可以顺利地求出Controlling UEP，但是也不能将e 取得过大。所以BLE系统中求取Controlling UEP仍是非常困难的。不过，一些特殊的算法，如DASSL^[20]可能会对此有所帮助，但仍需进一步研究。

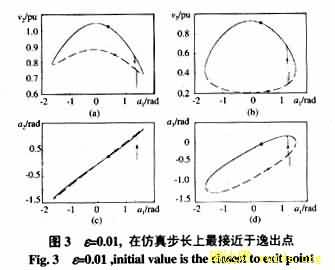
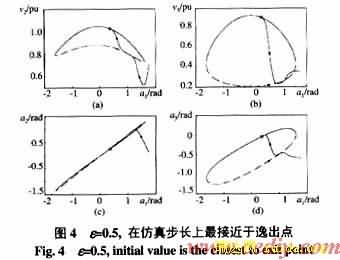
        2）求取DAE系统的Controlling UEP。
    尽管在L_h没有UEP，但是L_h边界是死巷点。故障后轨迹撞到死巷点仍然是危险的，运用文[16]提出的势能方法，用相关死巷点I_S的能量函数值替代Controlling UEP，来作为DAE系统暂态稳定判定的临界能量。根据虚拟持续故障跳变轨迹可得相关的死巷点为(1.636,1.282,0.724, 0.003,0.433)。
   （2）求取临界能量函数值
    应用文[5],[16],[18],[21]定义的能量函数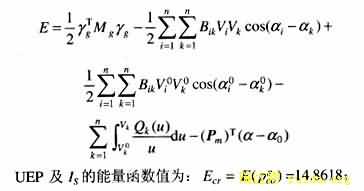

则求取临界能量函数值的步骤为：
    1）求取故障切除点及其对应虚拟跳跃点的能量函数值实际故障轨迹末值为p＝ (1.15,0.48,0.29,0.81, -0.33,0.53)，其对应的外部跳变目标点为q＝(1.15,0.48,0.84,0.89,0.15,0.74)，则E(p)=11.4710,E(q)=8.9735。
    2）分别比较能量函数值
   定，如图5、6所示。

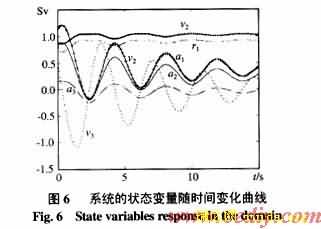
    例2  对图1所示系统，考虑母线B₂发生短路故障，且故障后系统与原系统保持一致。对于给定故障及实际故障轨迹末值，根据ECUEP方法，判断系统的暂态稳定性。
    其步骤如下：
   （1）同例1的步骤(1)。
   （2）该步骤分两步，
    1）实际故障轨迹末值为p=(1.48,0.56, 0.30,0.61, -0.40,0.37)，其对应的外部跳变目标点为q=(1.48,0.56,1.12,0.79,,0.14,0.59)，则E(q)= 14.8441,E(p)= 24.6886；
   2） 但E(P)>E_cr，所以故障后系统不稳定，如图7、8所示。故障后轨迹趋于一不可运行的稳定平衡点(0.628,0,0.466,0.845,-3.820, -0.215)。

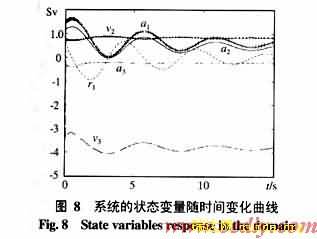
    注2  由图7可知，故障后轨迹没有降落到L_h上，系统不稳定。而仅根据虚拟跳跃目标点判定，故障后系统应该是稳定的。从图中可以看出，对外部跳跃的方向作出判断是必要的。否则,仅考虑DAE系统的子模式x=f[x,h(x)]会引起故障后系统稳定性的误判。
4  ECUEP方法的改进
    针对例1和例2，使用ECUEP方法及文[7]给出的概念性结构保持BCU方法分别进行暂态稳定分析，判定过程和结果比较如表1。
    由表1可见，就本章给出的例子，文[7]给出的BCU方法能够与ECUEP方法获得相同的判定结果，但计算量却减少一半。而且，由于Controlling UEP方法的保守性，使用它在进行外部跳变判定时常常出现保守的误判。

    根据文[15]中的定义2，BLE轨迹会在很短时间内逼近DAE的某一代数子流形，那么通过数值仿真，可以仅对BLE系统计算若干个步长便能够得到外部跳变方向及降落的代数子流形。如果假定仿真中不存在数值问题，那么，运用数值仿真的方法来判定外部跳变不仅可以克服Controlling UEP方法的保守性，而且也可以迅速地获得结果。对BLE系统的仿真目的在于：判定外部跳变行为时，只需仿真至能够获得结果便可停止，所以它与以前所说的用时域仿真方法来判定暂态稳定性是有区别的。
    综上所述，对ECUEP方法进行改进，可引入数值计算方法来判定外部跳变行为。将改进后的ECUEP方法称为混合ECUEP方法（Hybrid ECUEP Method），其步骤如下：
    （1）外部跳变行为的确定
    以p为初值，对故障后DAE系统所对应的BLE系统进行数值仿真，并根据BLE轨迹来判定故障后系统是否外部跳变至L_h。如果跳变至L_h，则需要步骤2和3的进一步判定；如果不跳变至L_h，则判定故障后系统不稳定。
    （2）临界能量的确定
    1）由持续故障轨迹对应的虚拟持续故障跳变轨迹，找到DAE的Controlling UEPp_0,co；

    （3）稳定性判定

    例3  对图1所示系统，考虑母线B₂三相短路故障，且故障后系统与原系统保持一致。对于给定故障及实际故障轨迹末值，根据Hybrid ECUEP、ECUEP和文[7]给出的BCU方法，分别判断系统的暂态稳定性。
    首先，使用Hybrid ECUEP方法进行暂态稳定判定。其步骤为：
    （1） p＝(1.25,0.50,0.29,0.75,-0.35,0.50)，计算得到跳变降落代数子流形为L_h；
    （2）此例使用与例1相同的系统，只是增大故障的持续时间，所以根据例1可知，18.1323；

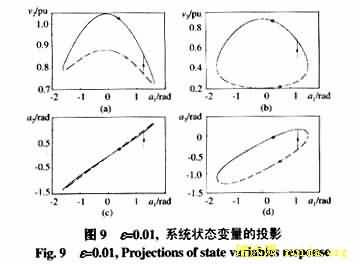
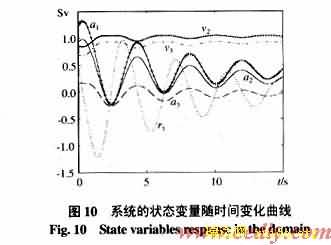
    例4使用ECUEP方法及文[7]给出的BCU方法进行暂态稳定判定。此例使用的系统与例1相同，仅增大故障的持续时间，其步骤为：
    （1）同例1步骤（1）。
    （2） p＝(1.25,0.50,0.29,0.75,-0.35,0.50)，其对应的外部跳变目标点为q＝(1.25,0.50,0.92,0.86,0.16,0.70),则E(q)=10.6447,E(p)=18.5751。
    （3）所以使用ECUEP方法及文[7]给出的BCU方法都判定故障后系统不稳定。
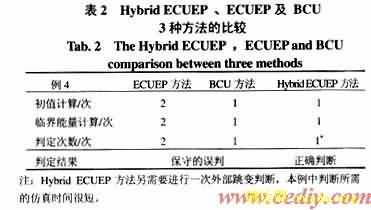
    针对例3，分别使用Hybrid ECUEP方法、ECUEP方法及文[7]给出的概念性结构保持BCU方法进行暂态稳定分析，分析结果见表2。由表2可见，对例3而言，ECUEP方法和文[7]给出的BCU方法得出了保守的误判，Hybrid ECUEP方法判定正确。与ECUEP方法相比，Hybrid ECUEP方法不仅改善了保守性，而且判定过程得到简化；与文[7]给出的BCU方法相比，Hybrid ECUEP方法有限地增加了判定时间，但可以换来更加准确的判定。

5  结论
    本文概述了现有基于结构保持模型的判定方法及存在的问题。在结合两者优点及文[16]定理3的基础上，提出了新的稳定性判定方法，并给出了具体算例，得出如下结论：
    （1）以传统Controlling UEP方法为依托，结合现有两种分析方法的优点，在对外部跳变行为讨论的基础上，提出新的基于结构保持模型的暂态稳定分析直接法——扩展Controlling UEP方法。
    （2）在ECUEP方法的基础上，以数值仿真来替代一部分能量函数的比较，提出Hybrid ECUEP方法，从而提高了判定的实用性与准确性。
    附录A：引理1的证明

    附录B 定理1的证明

附录C  定理2的证明

                                        参考文献

[1]    Bergen A R, Hill D J, A structrue preserving model for power system stability analysis[J].IEEE Trans. on Power Apparatus and Systems, 1981,PAS-100：25-35.
[2]    Narasimhamurhi N, Musavi M R. A general energy function for transient stability analysis of power systems[J]. IEEE Trans. on Circuits and Systems, 1984,CAS-31：637-645.
[3]    Tsolas N A, Arapostathis A, Varaiya P P. A structure preserving energy function for power system transient stability analysis[J]. IEEE Trans. on Circuits and Systems, 1985, CAS-32：1041-1049.
[4]    薛禹胜，运动稳定性量化理论[M].南京：江苏科学技术出版社.
[5]    Hiskens I A, Hill D J, Energy functions, transient stability and voltage behavior in power systems with nonlinear loads[J].IEEE Trans. on Power Systems, 1989,4(4)：18-22.
[6]    Hill D J, Mareels I M Y. Stability theory for differential/algebraic systems with application to power systems[J]. IEEE trans. on Circuits and Systems, 1990,CAS-37：1416-1422.
[7]    Chiang H D, Chu C C, Cauley G., Direct stability analysis of electric power systems using energy functions: theory, applications, and perspective[J]. Proceedings of the IEEE, 1995,38(11)：1497-1529.
[8]    Chiang H D, Hirsch M W, Wu F F, Stability region of nonlinear autonomous dynamical systems[J]. IEEE Trans. Auto. Contr., 1988，AC-33(1)：16-27.
[9]    Chiang H D, Fekih-Ahmed L, On the direct method for transient stability analysis of power system structure preserving models[A].IEEE International Symposium on Circuits and Systems[C]. 1992：2545-2548.
[10]De C L Marco， Bergen A R. A security measure for random load disturbances in nonlinear power system models[J]. IEEE Trans. on Circuits and Systems, 1987 ,CAS-34：1546-1557.
[11] De C L  Marco, Bergen A R. Application of singular perturbation techniques to power system transient stability analysis[A]. IEEE International Symposi um on Circuits and Systems[C]. 1984：597-601.
[12] Sastry S S, Varaiya P. Hierarchical stability and alert state steering control of interconnected power systems[J]. IEEE Trans. on Circuits and Systems, 1980,CAS-27, 11.
[13] Bergen A R, Hill D J, Demacro C L. Lyapunov function for multimachine power systems with generator flux decay and voltage dependent loads[J]. Electrical Power and Energy Systems, 1986,8(1)：36-41.
[14] 贺仁睦, 王卫国, 蒋德斌, 等(He Renmu,Wang Weiguo, Jiang Debin, et al). 广东电网动态负荷实测建模及模型有效性的研究(Measurement-based dynamic load modeling and moder validation of guangdong grid)[J]. 中国电机工程学报(Proceedings of the CSEE), 2002,22(3)：78-82.
[15] 殷明慧,  邹  云(Yin Minghui，Zou Yun). 电力系统结构保持模型相关不稳定平衡点方法的理论(Controlling uep method in network structure preserving power system model)[J].中国电机工程学报(Proceedings of the CSEE), 2003,23(8)：32-37.
[16] Praprost K L, Loparo K A. An energy function method for determining voltage collapse during a power system transient[J]. IEEE Trans. on Circuits and Systems, 1994,CAS-41：635-651.
[17] Sastry S S, Desoer C A. Jump behavior of circuits and systems[J]. IEEE Trans on Circuits and Systems, 1981,CAS-20, 12.
[18] 余贻鑫, 王成山. 电力系统稳定性理论与方法[M].北京：科学出版社.
[19] 王成山 贾宏杰 江晓东(Wang Chengshan, Jia Hongjie,Jiang Xiaodong). 一种寻找正确相关不稳定平衡点的基准方法(Standard method for finding correct controlling unstable equilibrium point)[J]. 天津大学学报(Journal of Tianjin University), 1999,32(5)：509.
[20] Brenan, K E, Campbell S L, Petzold L R. Numerical solution of initial-value problems in differential-algebraic equations[M]. SIAM, Philadelphia, 1996.
[21] 房大中, 周保荣, 宋文南, , 等(Fang Dazhong, Zhou Baorong,Song Wennan, et al). 修正的暂态能量裕度评估策略(Atrategy for assessment of corrected transient energy margin)[J]. 中国电机工程学报(Proceedings of the CSEE), 2002, 22(3)：94-98.