打印本文 
关闭窗口 关键词：电容式电压互感器； 暂态噪声模型； 衰减因子
1 引言
在超高压输电线路上，由于经济、技术等方面的原因，通常采用电容式电压互感器（CVT）作为电压变换元件，输出较低电压供保护和测量元件使用。这种电压互感器暂态特性差，当一次侧发生近距离短路时，输出的二次电压中含有大量的噪声，有可能使继电保护装置误动作。因此，有必要对CVT的暂态噪声进行研究，找出其中的规律；这对于消除噪声的影响，研究新的保护算法是非常有意义的。CVT暂态过程的研究，已做了很多的工作，但主要集中在CVT参数和负载变化对暂态过程大小的影响。本文则从建立CVT暂态噪声模型入手，深入研究了暂态噪声的组成、变化规律以及频谱特点，得到了一些有价值的结果。
2 CVT的等效电路
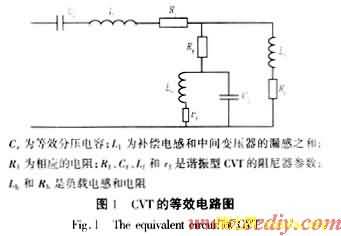
CVT由分压电容、补偿电抗器、中间变压器、阻尼器等部分组成。本文是研究系统短路故障时CVT的暂态过程。系统短路故障时，电压降低，中间变压器的铁心不会饱和，其励磁回路对CVT暂态过程的影响可以忽略。因此CVT的等效电路可以由图1来表示。为了提高测量精度，在工频下Cf与Lf处于并联谐振状态，Ce与L1也近似处于串联谐振状态。
3 CVT的暂态噪声
设CVT一次和二次电压分别为u和u2。相应的拉普拉斯变换为U（s）和U2（s），从图1知CVT等效电路是一个线性系统，因此可表示为
式（1）中，G（s）为CVT的传递函数。
根据叠加原理，故障后CVT的一次电压可表示为
式（2）中u（0）是系统正常运行电压，Δu是故障分量电压。
对式（2）进行拉普拉斯变换，得
式（4）中L－1（）为拉普拉斯反变换的符号。
考虑到u（0）是稳态量，将一次电压和二次电压归一化（以系统额定电压为基值），并忽略CVT的稳态测量误差后，不难知
综合式（5）、式（4）和式（2）的结果，得
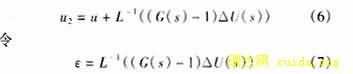
显然，ε就是CVT的暂态噪声。为了进一步分析ε，设t＝0时刻发生故障，故障前后的CVT一次电压分别为
由于电压是采用归一化表示的，因此式（8）中假设了故障前电压u（0）的大小等于系统的额定电压，而U则是故障后测量点的残压与系统额定电压的比值，显然U＜1。就是故障角，φd是故障前后电压相位的变化。如果系统阻抗与线路阻抗的阻抗角相等，金属性故障时φd＝0°，线路出口经小电阻故障时φd最大可达90°。将式（8）和式（9）代入式（2），可得故障分量电压为
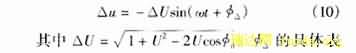
达式当然也可以从式（8）和式（9）中求出，但无必要。只需注意一点：Δ在金属性故障时就等于故障角；经过渡电阻故障时则与故障角不相等。
将式（10）进行拉普拉斯变换后代入式（7），得
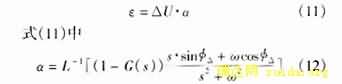
从式（11）知，CVT的暂态噪声ε与电压的故障分量ΔU成简单的正比关系，ε在故障后的变化规律则取决于α。由于故障暂态过程结束后暂态误差ε＝0，而对于某个具体的故障ΔU是个常数，因此α是一个逐渐衰减到0的量，本文称之为衰减因子。
α不但与CVT参数有关，也与故障的初始角度φΔ有关。
4 暂态噪声的变化规律
下面是一组典型的CVT参数［1］，各参数已折算到一次侧。
CVT的额定负荷为：Rb＝1352 kΩ；Lb＝3229 H；
根据这些参数和图1电路，运用MATLAB仿真计算工具，求得CVT的传递函数为
从式（14）和（15）中可以看到，α由低频分量、高频分量和非周期分量组成，它们的衰减时间常数分别为τ1、τ2和τ3，大小主要由CVT的参数决定。由于时间常数τ1≥τ2，τ3，因此低频分量在α中起主导作用。其它两个分量衰减很快，只在故障开始几个毫秒内起作用。φΔ的不同会显著影响α中各分量的幅值和初相角，但不会影响各分量的频率和衰减时间常数。由于低频分量占主导地位，CVT的暂态噪声主要取决于低频分量的幅值A和初相角φ1。根据式（14）和（15）可以算出φΔ＝0°时，A＝0．5927，
＝90°时幅值比0°时下降了将近一半。另外φΔ＝90°时正弦函数值是下降的，考虑到幅值的衰减，更加降低了噪声水平。图2是两种φΔ下α的波形，图中的虚线是低频分量的波形。从图2中可以看到，φΔ＝0°故障时，CVT的暂态噪声要比90°时严重得多，另外故障5ms后，低频分量的波形与α已经很接近了。
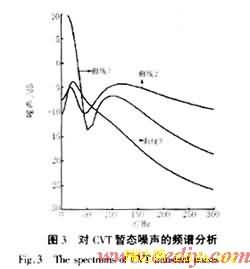
图3是α的频谱。曲线1是φΔ＝0°时的情况，主要由低频分量组成。曲线2是φΔ＝90°时的情况，频谱范围比较广，但从图2中可以看到，此时α可以分为两个时间段，故障刚开始阶段主要是高频分量；故障5ms后高频分量已经衰减了很多，同时低频分量逐渐增大并重新占据了主导地位，而此时低频分量也有了一定的衰减，因此整个暂态噪声水平比较低，图3的曲线3就是在α中剔除前5ms波形后的频谱，高频分量已经很小了。因此要减少暂态测量误差，重点是消除低频分量的影响。
5 负载和CVT参数对暂态噪声的影响
对于不同的实际系统，CVT的负载是不一样的。不同型号的CVT产品，其参数也会有差异。表1列出了CVT参数和负载改变时暂态噪声各特征量的变化情况。由于Cf与Lf、Ce与L1在工频下要处于谐振关系，因此在Cf或Ce改变时Lf或L1也相应的作了改变。表1中各分量的幅值是φΔ＝0°时的计算结果。
从表1中可以看到，在CVT的参数和负载变化时，有
1）非周期分量的幅值（K5）比较小；基本上在额定电压的10％以下，再考虑到其衰减时间常数（τ3）较小，因此其对CVT输出的影响较小；
2）负载变化时低频分量（f1）和高频分量（f2）的频率变化很小，f1基本上在17 Hz左右变化，f2基本上在90 Hz左右变化；低频分量的衰减时间常数（τ1）比较大，在11 ms左右变化，高频分量的衰减时间常数（τ2）比较小，在2～3ms之间。因此在CVT的参数和负载变化时，低频分量和高频分量在暂态 噪声中的地位没有改变。
3）负载的容量变化对暂态噪声的影响小，但功率因数的变化对低频分量和非周期分量的衰减时间常数影响比较大，特别是非周期分量非常敏感（从额定时的2 ms变化到功率因数为0．1时的14 ms）。功率因数低时时间常数增大，使CVT的暂态过程衰减变慢。在CVT负载不大的系统，人为地增加一些电阻性负载有助于减少测量误差。
4）在CVT的分压电容和阻尼参数变化时，虽然衰减时间常数和频率跟额定时比较变化较大，但暂态噪声各分量的构成和低频分量占主导地位的特点没有改变。
6 结论
CVT的暂态噪声与电压故障分量的大小成正比，可以由一个低频分量、高频分量和非周期分量的模型来表示。其中低频分量占主导地位，高频分量衰减很快，一般只在故障后5ms内发生作用。负载的变化对CVT暂态噪声各分量的频率影响很小，但负载功率因数对非周期分量的衰减时间常数影响很大，功率因数低时暂态过程更加严重。故障角不会影响暂态噪声的频率和衰减时间常数，但会影响各分量的幅值和初相角，在电压过零附近故障时暂态噪声严重。
本文的结果为提高快速保护的电压测量精度提供了新的研究思路。例如在CVT负载不大的系统，人为地增加一些电阻性负载有助于减少测量误差；根据CVT暂态噪声主要是低频谐波的特点，在保护算法中增加一个低阻滤波器，可以有效地减少CVT的暂态测量误差；采用信号处理技术，在测量电压波形中实时辨识出CVT暂态噪声各分量的参数，进而消除其影响。通过厂家提供的CVT参数和实测的负载参数，可以离线计算出暂态噪声中各分量的频率和衰减时间常数，因此在实时参数辨识时，需要辨识的只是各分量的幅值和初相角（或相量）。若不采用实测的负载参数，考虑到各分量的频率在负载改变时变化很小，因此频率还是可以离线计算出，而通过电压波形实时辨识出各分量的幅值、初相角以及衰减时间常数。
打印本文 关闭窗口