摘 要:根据双向晶闸管和触发二极管的伏安特性和典型应用电路的工作原理,列出了电路方程,并应用计算机求得了功率调节系数与时间常数RC的数值解,通过对数值解进行分析,得出了线性调节范围。并讨论了最大时间常数与触发二极管参数之间的关系。
关键词:双向晶闸管;触发二极管;相位控制角;功率调节系数
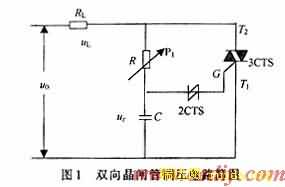
由双向晶闸管3CTS和触发二极管2CTS (又称为二端交流元件DIAC)组成的调压电路,略去辅助元件后的电路如图1所示,大量地用在民用电器中的调光、调温。对于调节原理,查阅相关报道[1~3],大多文中对触发原理仅做出定性的说明,没有定量结论。本文在对触发原理讨论的基础上,求解了控制参量R,C与输出电压或输出功率的定量关系,在此基础上,还就线性范围进行讨论,期望此结论能对应用起到参照作用。
1调压原理讨论
双向晶闸管调压电路中忽略一些辅助元件后的电路如图1所示。图2是触发二极管2CTS的伏安特性,其中OP段为截止区;PV段为负阻区,VP1段为饱和区。3CTS导通受控于2CTS产生的触发脉冲电流,而2CTS只有在uc增加到UP后,由于P-V段负阻区,引起强烈的正反馈,又因uc不能突变,故瞬间使工作点由P点跳变至P1点,此刻2CTS中有电流i,当脉冲电流峰值Im大于3CTS的触发电流时,3CTS便导通。
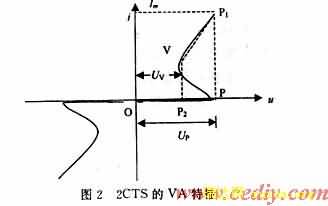
此后,电容C的放电回路有2条,一条是:C-R-T2-T1-C;第二条是:C-2CTS-G-T1-C。由于处于饱和区的2CTS饱和电阻远小于R,所以放电时间常数主要由第二条回路决定。很短时间uc便由UP退至UV,2CTS的工作点便由P1点移至V点。进入负阻区V-P段后,又是一个正反馈使工作点跳变到P2,uc=UV。这时2CTS重新截止。随后,电容仅通过第一条支路放电,uc呈指数规律下降,当输入的端电压瞬时值过零时刻T/2,uc=uc(T/2),此时3CTS也自动截止。此后,uc又开始了在正弦输入电压激励下,以初值uc(T/2)的反向充电过程。图3中画出了以端电压ui(t)过零时刻为t=0时,uc(t)、负载上的电压uL(t)以及过2CTS的触发电流i随时间t的变化曲线。
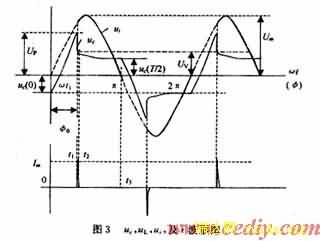
2控制角φ与电路参数RC之间的定量关系
图3中,0-t1段uc的形成是在正弦电压ui=Umsin ωt的激励下,由初始值uc(0)开始的充电过程。这段时间内2CTS与3CTS都截止,其等效电路如图4所示。考虑到RL<
![]()
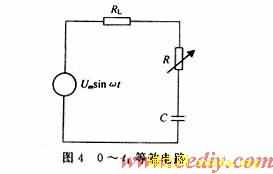
t2~t3段中3CTS处于导通状态,可看作电容通过第一条支路的放电过程,放电时间常数为RC。所以,u(t)呈指数规律下降,uc(T/2)应满足下式。![]()
考虑到ui(t)和3CTS与2CTS的伏安特性的对称性,必有: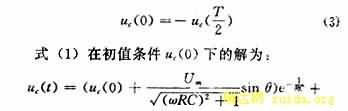
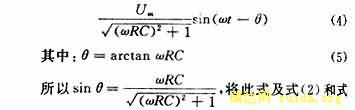
(3)代入式(4),并令:
式(6)为元件参数RC与与相位控制角φ之间的定量关系。
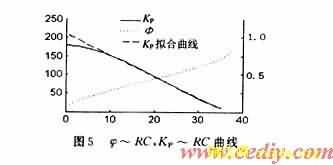
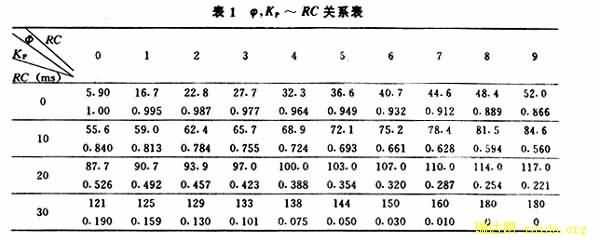
由于此方程为超越方程,不能直接求得φ~RC的解析表达式,但可在给定Um,ω,UP,UV之后,用计算软件Matlab 6.0求得其数值解,表1是以Um=311V;UP=31.4V;UV=20V;ω=100πrad/s时由式(6)计算的结果。在图5中画出了φ~RC曲线。他们的关系如表1所示。
3功率调节系数KP与电路参数间的关系
由于该电路一般都用作功率调节,由图3的波形可知负载电阻RL上的电压有效值: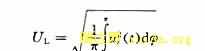
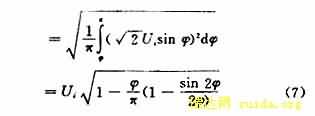
定义功率调节系数:![]()

利用φ~β(=ωRC)的数值计算结果,可求得KP与RC之间的定量关系。
4KP的线性范围的讨论
(1) 从图5中φ~RC与KP~RC曲线可以看出,在RC较小和较大时线性较差,在KP为0.9~0.05部分有较好的线性范围,可用Matlab 6.0对KP~RC中部进行直线拟合得:KP=1.167 6~0.032 3(RC)。
这个结果说明,用触发二极管触发的双向晶闸管电压调节电路,用于纯阻性电路中作功率调节时,欲使功率呈线性变化,用线性电位器作调节元件是较好的选择。
以上结论经实际测试,其结果与理论计算吻合。
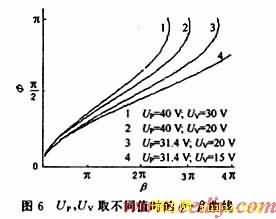
(2)用Matlab 6.0软件,当式(6)中UP,UV取不同值时,作φ~RC曲线,如图6所示。从图中看出,电路中最大RC值(RC)max以及与之相应的KP线性范围与UP,UV以及其差值有关,UP,UV愈大,(RC)max愈小。
参考文献
[1]钱博森负阻器件负阻电路及其应用[M]天津:天津大学出版社,1993
[2]郗建平双向晶闸管调光电路[J]安装,2001
[3]艾斌双向可控硅的触发[J]达县师范高等专科学校学报(自然科学版),2000,(6)
[4](美)R F 格拉夫电子电路百科全书(第1卷)[M] 电子电路百科全书翻译组译,北京:科学教育出版社,1991
[5]康华光电子技术基础上册[M]北京:人民教育出版社,1982
[6]张永瑞电路分析基础[M]西安:西安电子科技大学出版社,1987
|
|
|