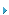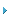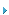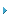图14 是用MathCad 工作表根据在4,000MHz 上所测量巴伦的数据来计算差分阻抗的一个例子。差分阻抗的计算和结果曲线的绘制可能是很繁琐的,特别是对于宽带应用来说。在这种情况下,一个好的射频仿真程序可能会有所帮助。图15 是ACS的功能强大且价格并不昂贵的射频仿真器的LINC2 的仿真例子。为方便起见,还显示出了仿真电路图,其中包括了二端口黑盒子S1,这个黑盒子是与一个被测S-参数文件和2 个不平衡的50Ω 端口有关的。解出的差分阻抗显示在史密斯圆图的左边,对应的频率和单端口阻抗(每个端口对地)用4 个标记列在史密斯圆图的下方。LINC2 将所有类型的阻抗用串联形式来表示。可以很容易地用(21)-(22)将其转化为并联形式。仿真结果显示出感抗是接近于零的(与Math-Cad计算相比较)。当感抗不等于零时,原因可能在于校准得不完美以及测量中的某些不确定因素。在这种情况下, 如果需要更高的精度, 则要在巴伦的差分端口加上相反符号的感抗后进行重复测量(管脚2 和3)。然后,新获取的S-参数文件必须要再次插入射频仿真器中,此时便可以得到差分阻抗的正确值。文献[3] 对此方法进行了解释。